F_s = c･W₀

where:

F_s = Shear force acting at basal level
c = Design coefficient for seismic forces, the value is dependent of
      the seismic analysis method used
W₀ = Load or total weight of building

The seismic coefficient of the structure can be calculated by the static equivalent method, as follows:

c=

V0 W0

=

S(2.7*a0) Q'Ω

The coefficient c, always shall be higher that (S)(a₀)

where:

S = Amplification factor due to soil type (see Table 1 and Table 2, and Figure 1)
a₀ = Peak ground acceleration, its value is correspondent to
       spectral acceleration when the period of the estructure is zero
       (T = 0) (see Figure 2 & Table 3)
Q' = Reduction factor due to ductile behavior of the structure
Ω = Reduction factor due to overstrenght (Ω=2)

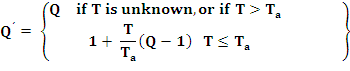
where:

Q = Ductile capacity of the structure (see Table 4)
T =
       (1) Fundamental period of the structure (static method)
       (2) Natural period of vibration of the correspondent mode
             considered, when the modal dynamic analysis be used.
T_a,T_b = characteristic period defined by the design spectrum
       (see Figure 2)

Spectrum for static analysis and dynamic analysis

For static and dynamic analysis, the acceleration value which shall be used will be determined as follows (See Figure 2):

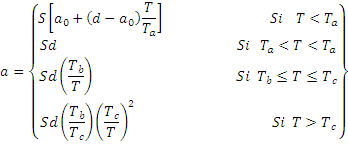
where:

S = Amplification factor due to soil type (see Table 1 and Table 2)
a₀ = Peak ground acceleration, its value is correspondent to
       spectral acceleration when the period of the estructure is zero
       (T = 0) (see Figure 2 & Table 3)
T =
       (1) Fundamental period of the structure (static method)
       (2) Natural period of vibration of the correspondent mode
             considered, when the modal dynamic analysis be used.
T_a,T_b,T_c = characteristic period defined by the design spectrum
       (T_a = 0.1s, T_b = 0.6s and T_c = 2 s) (see Figure 2)

Note:
For structures of Group B and C, a₀ will select from the isoacceleration map (see Figure 3)
For structures of Group A, a₀ coefficient shall be multiplied by 1.5