Tsunami Source Models of the 2011 Off the Pacific Coast of Tohoku Earthquake
(Ver. 6.2, Ver. 7.0 and Ver. 8.0)   


Old versions are here.


 

We performed multiple time-window tsunami waveform inversions to estimate the temporal and spatial distribution of fault slips of the Tohoku earthquake (38.322°N, 142.369°E, Mw = 9.0 at 5:46:23 UTC according to USGS) on March 11, 2011. We assumed 44 or 55 subfaults which are located within the aftershock area (Fig. 1). A rupture velocity of 2.0 km/s was assumed from the epicenter to an edge of each subfault.

Ver. 6.2: 44-subfault model. The length and width are 50 km × 50 km for each subfault. The focal mechanisms of the all subfaults are strike:193º, dip:14º and slip:81º from the USGS's Wphase moment tensor solution. The top depths of the subfaults were assumed to 0 km, 12.1 km, 24.2 km and 36.3 km for near-trench, shalow, middle and deep subfaults, respectively.

Ver. 7.0 [Satake et al., 2013]: 44-subfault model. The length and width are 50 km × 50 km for each subfault. The strike and slip angles are 193º and 81º, respectively, from the USGS's Wphase moment tensor solution. The dip angles are assumed from the plate boundary model [Nakajima and Hasegawa, 2006]. They are 8º, 10º, 12º and 16º from near-trench to deep subfaults. The top depths of the subfaults were assumed to 0 km, 7.0 km, 15.6 km and 26.0 km for near-trench, shalow, middle and deep subfaults, respectively.

Ver. 8.0 [Satake et al., 2013]: 55-subfault model. The near-trench subfaults are halved for the width (i.e. 25 km) from Ver. 7.0. The other fault parameters are the same with Ver. 7.0. The top depths of the subfaults were assumed to 0 km, 3.5 km, 7.0 km, 15.6 km and 26.0 km from near-trench to deep subfaults.

In order to calculate the Green's functions from source to stations, static deformations of the seafloor, the initial conditions for tsunami, were calculated for a rectangular fault model [Okada, 1985] for each subfault. The used bathymetry data are 30 arc-second grid from JTOPO30 for tide gauges in Japan and 2 arc-minute grid for off shore (Pacific Ocean), resampled from GEBCO_08 30 arc-second grid data. To calculate tsunami propagation, the linear shallow-water, or long-wave, equations were numerically solved by using a finite-difference method [Satake, 1995]. According to the inversion result, large slips are located around the epicenter and near the trench. The moment magnitudes of these source models are Mw 9.0. The comparison of tsunami waveforms are shown in Fig. 3. The tsunami waveform data were recorded at ocean bottom tsunami sensors of DART by NOAA, JAMSTEC and ERI, GPS wave gauges, tide and wave gauges by MLIT(NOWPHAS) and tide gauges of JMA, JCG, and tide or wave gauges at the Nuclear Power Plants. The calculated seafloor deformation from the inversion results are shown in Fig. 4. We can see the tsunami propagation to the northeastern coasts of Japan (Fig. 5).

Fault parameters are here (Ver. 6.2) and (Ver. 7.0) and (Ver. 8.0)


Snapshots of temporal slips on the faults are here (Ver. 6.2) and (Ver. 7.0) and (Ver. 8.0)



 

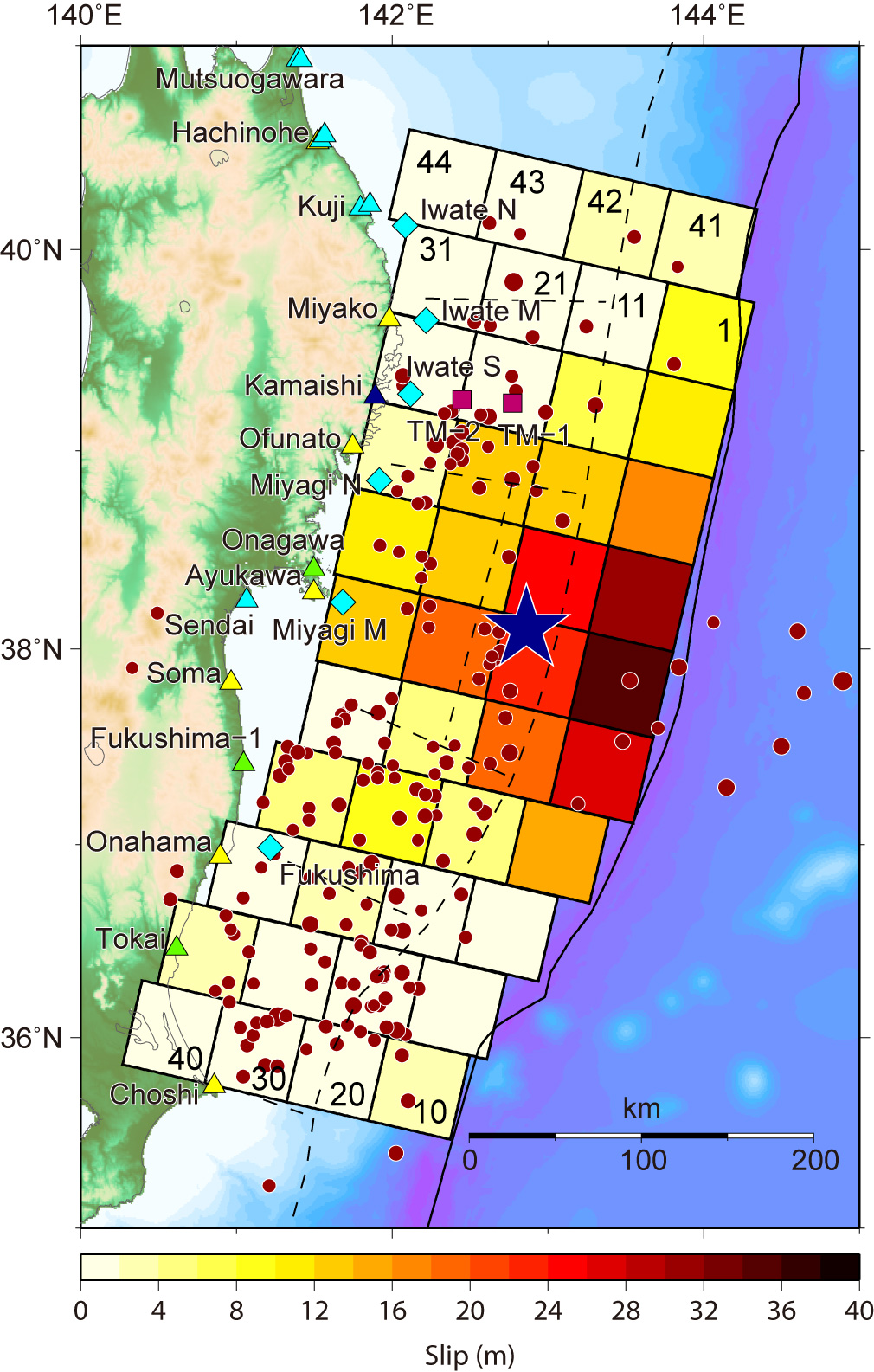
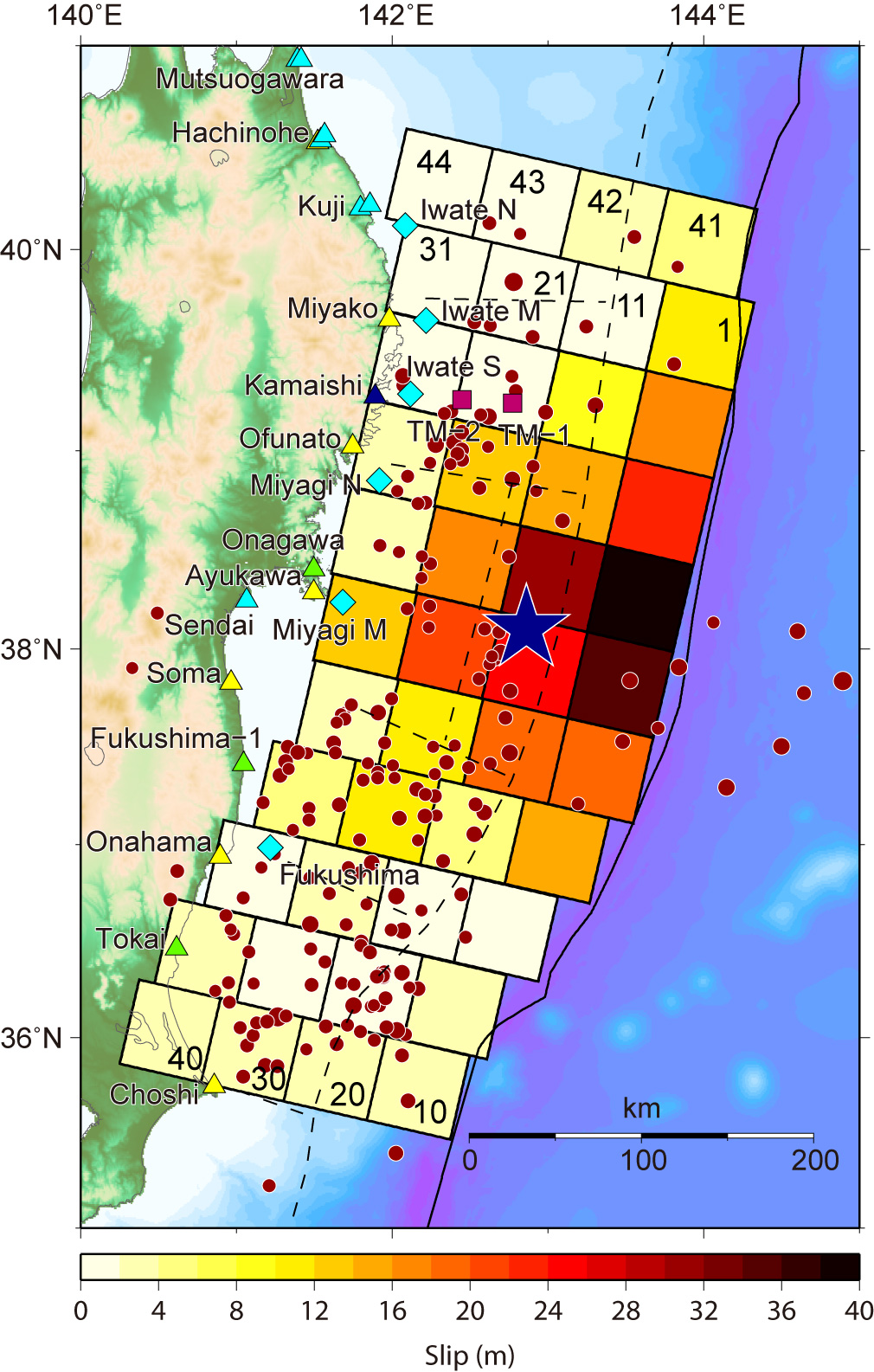
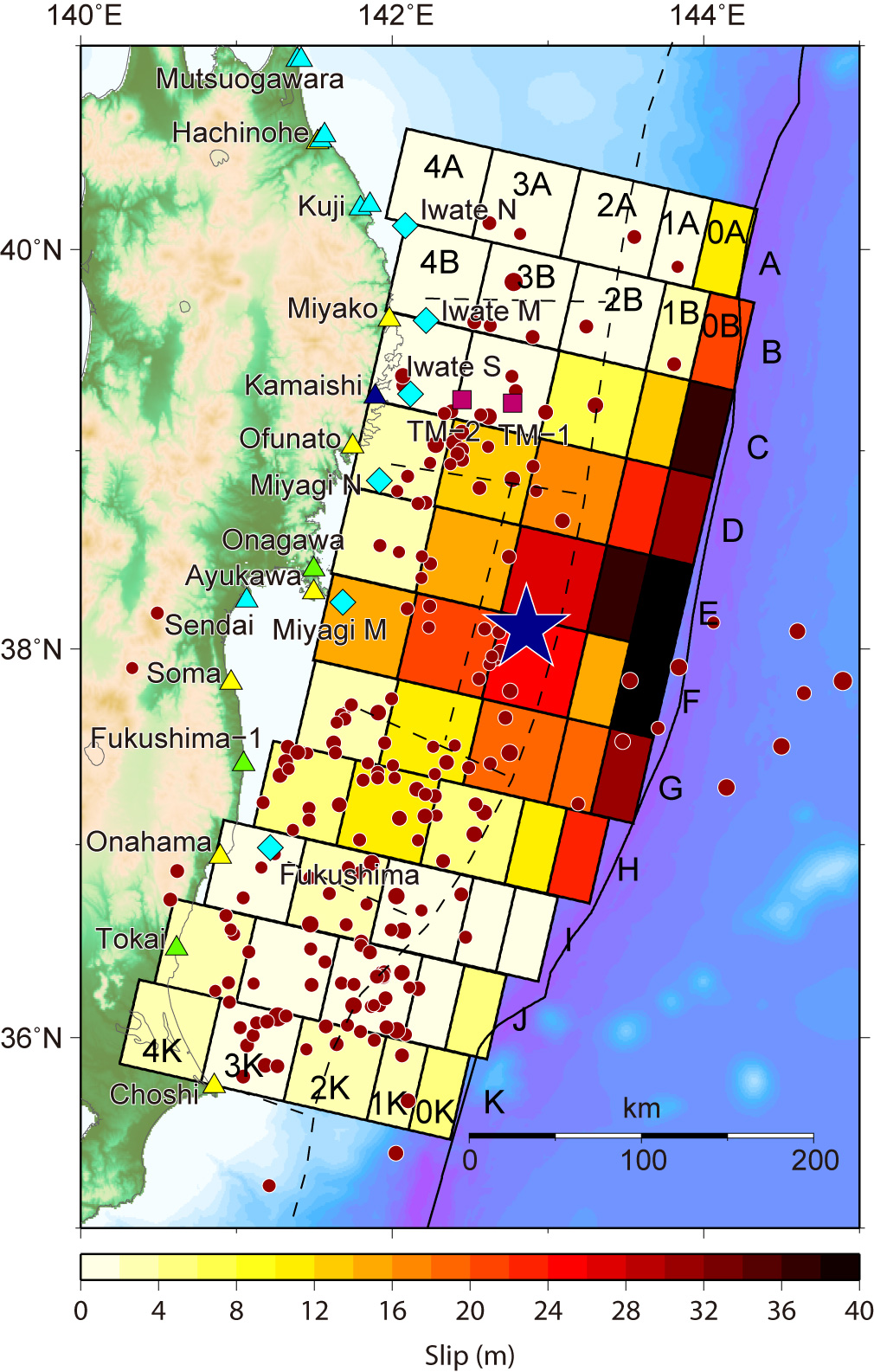
Fig.1 Tsunami Source Model Ver6.2 Fig.1 Tsunami Source Model Ver7.0 Fig.1 Tsunami Source Model Ver8.0

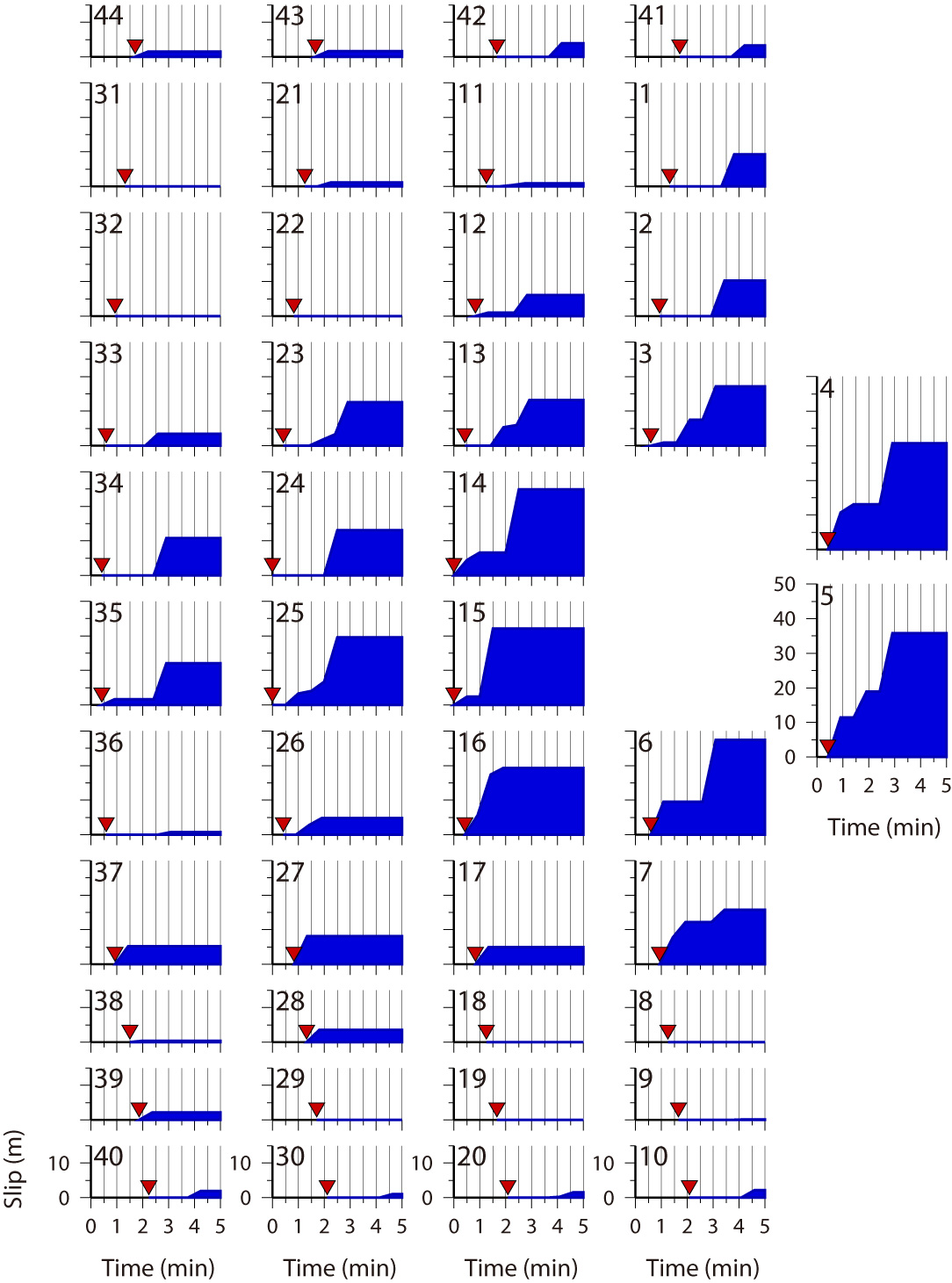
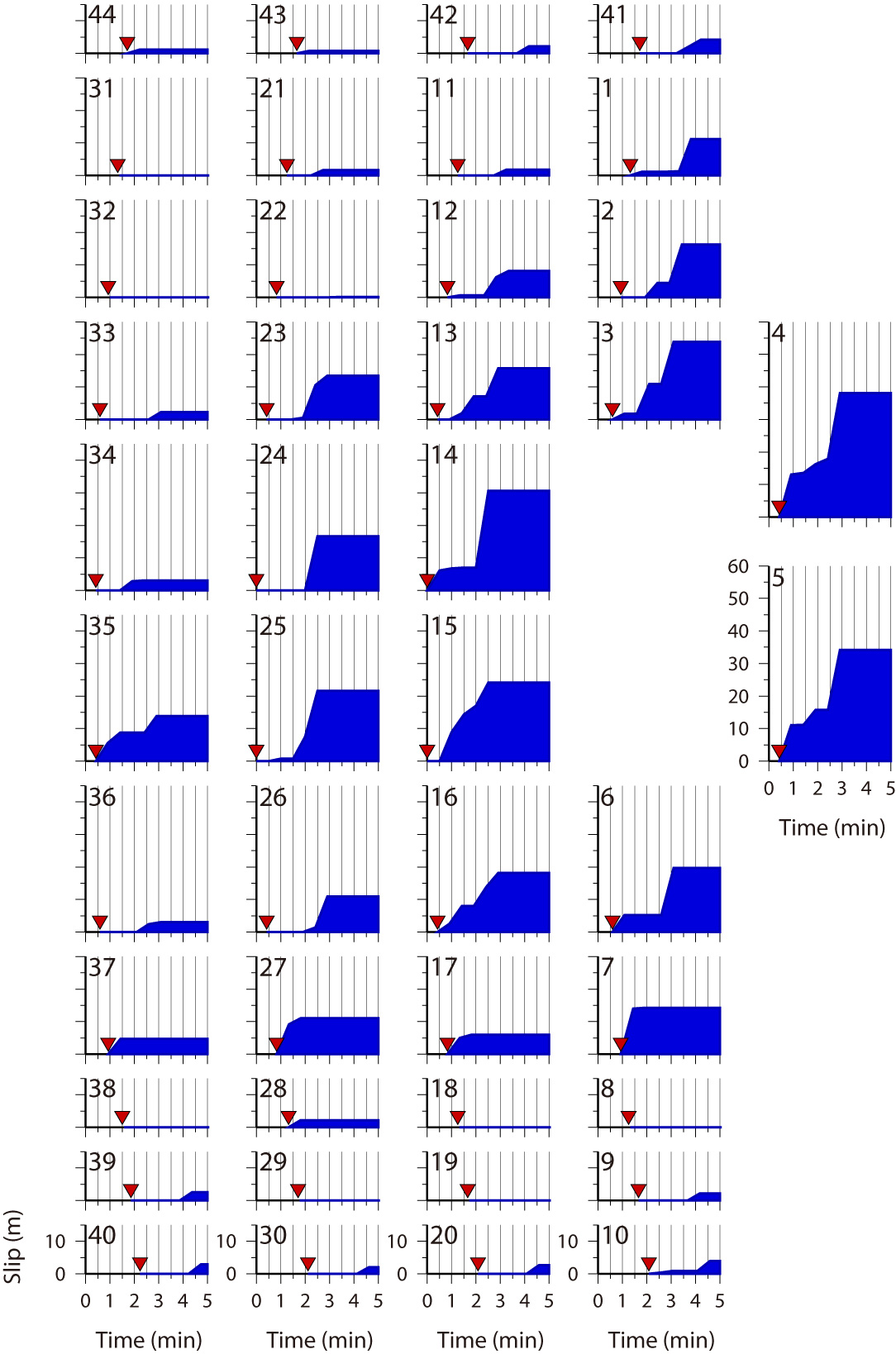
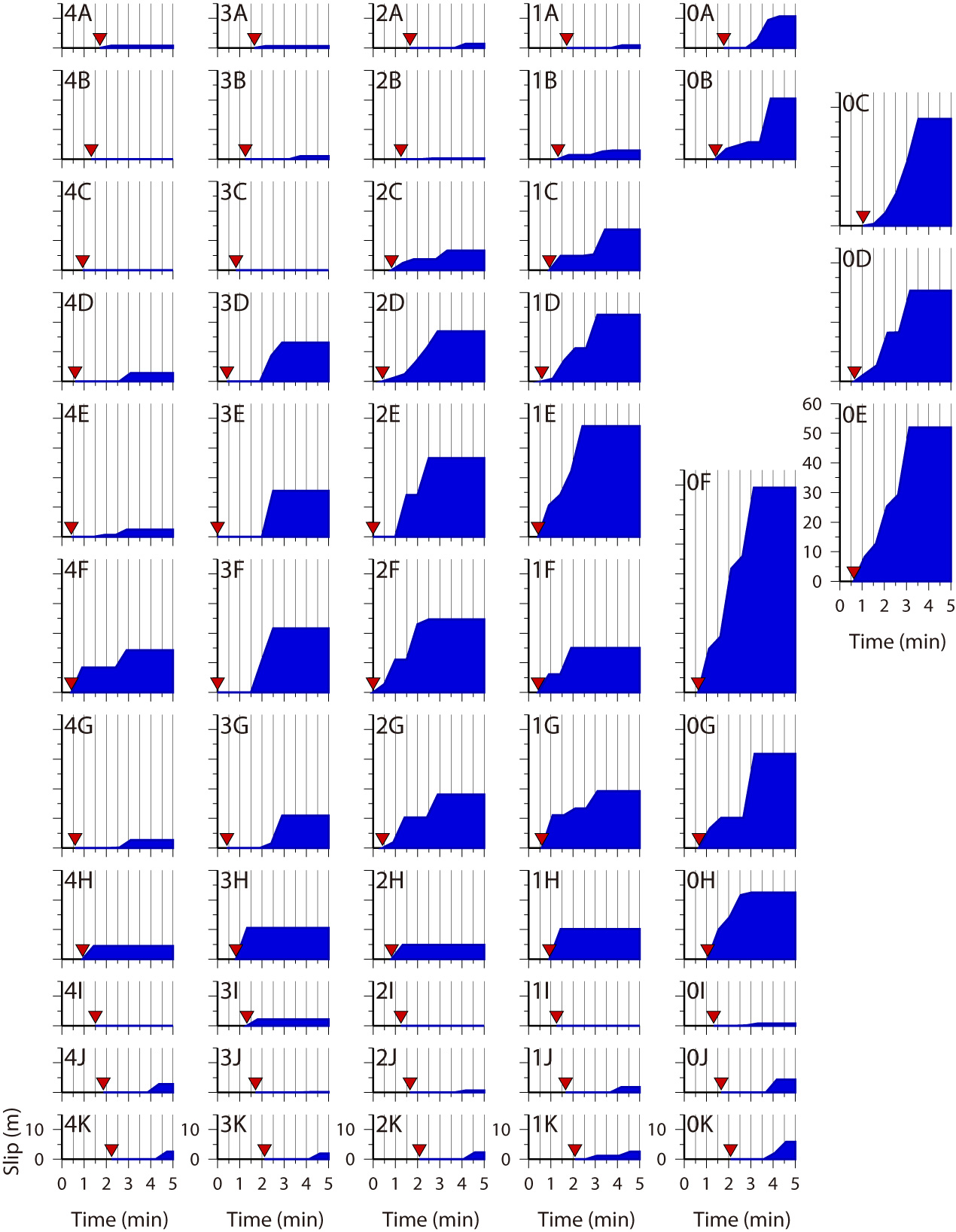
Fig.1 Tsunami Source Model Ver6.2 Fig.1 Tsunami Source Model Ver7.0 Fig.1 Tsunami Source Model Ver8.0

Fig.1 Tsunami Source Models, Left: Ver. 6.2, Middle: Ver. 7.0, Right: Ver. 8.0
 Upper: Slip distribution on the fault model. Mainshock (Blue star) and aftershocks (determined by JMA) during about one day after the mainshock are also shown by red circles.
Lower: Spatial and temporal distribution of slip on subfaults. Temporal changes of slip after the rupture onset (inverse triangles, assuming a rupture velocity of 2.0 km/s) with 30 s interval are estimated.


 

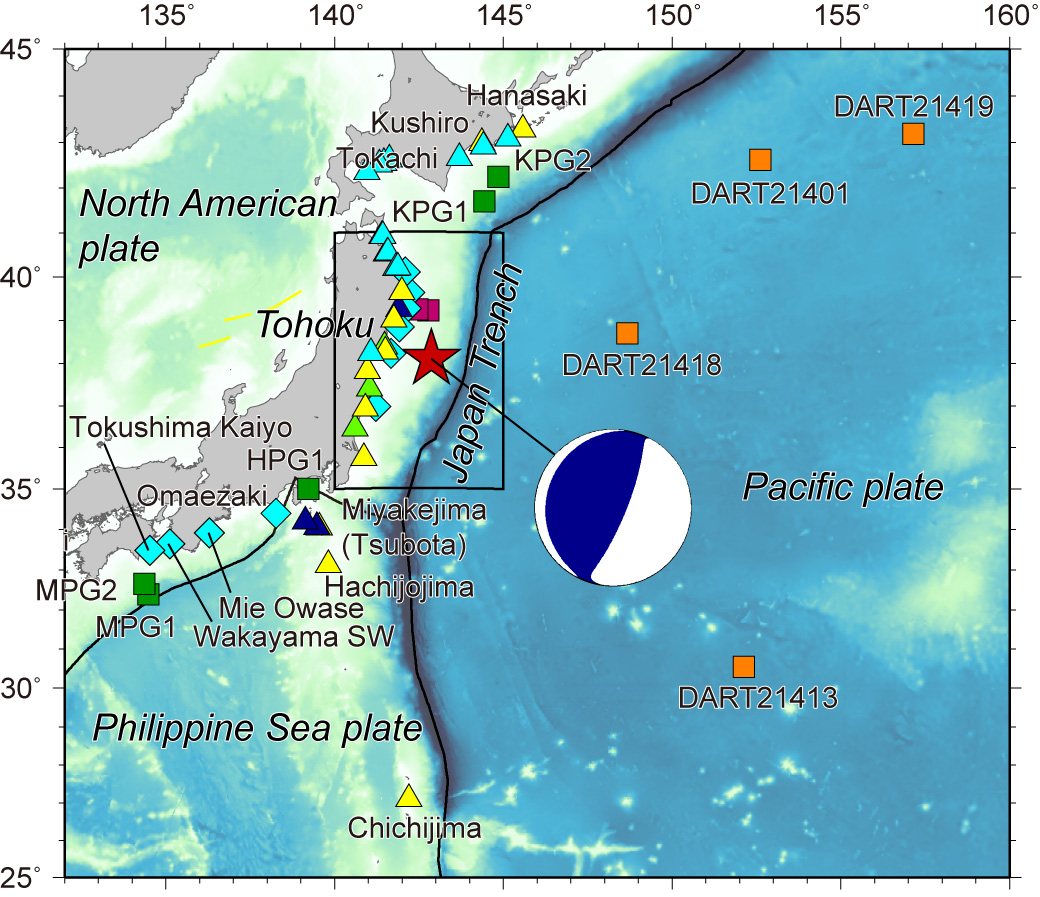
Fig.2 Offshore stations, tide and wave gauges

Fig.2 Offshore stations, tide and wave gauges used for the inversion.


 

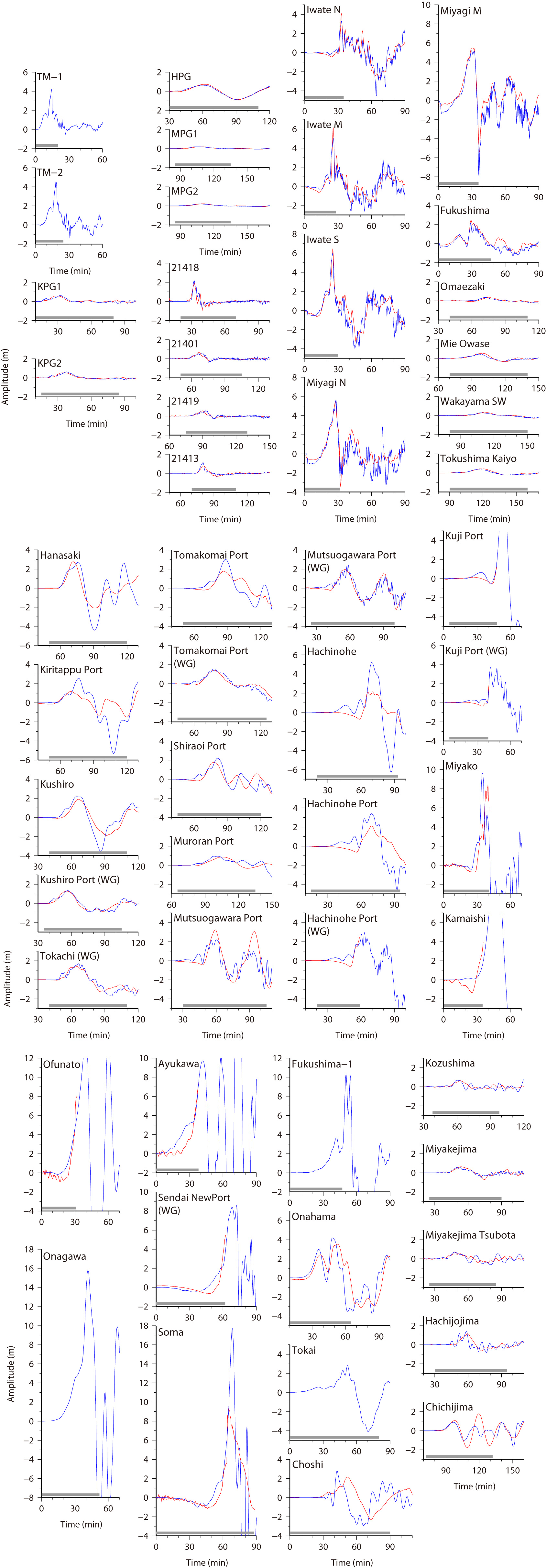
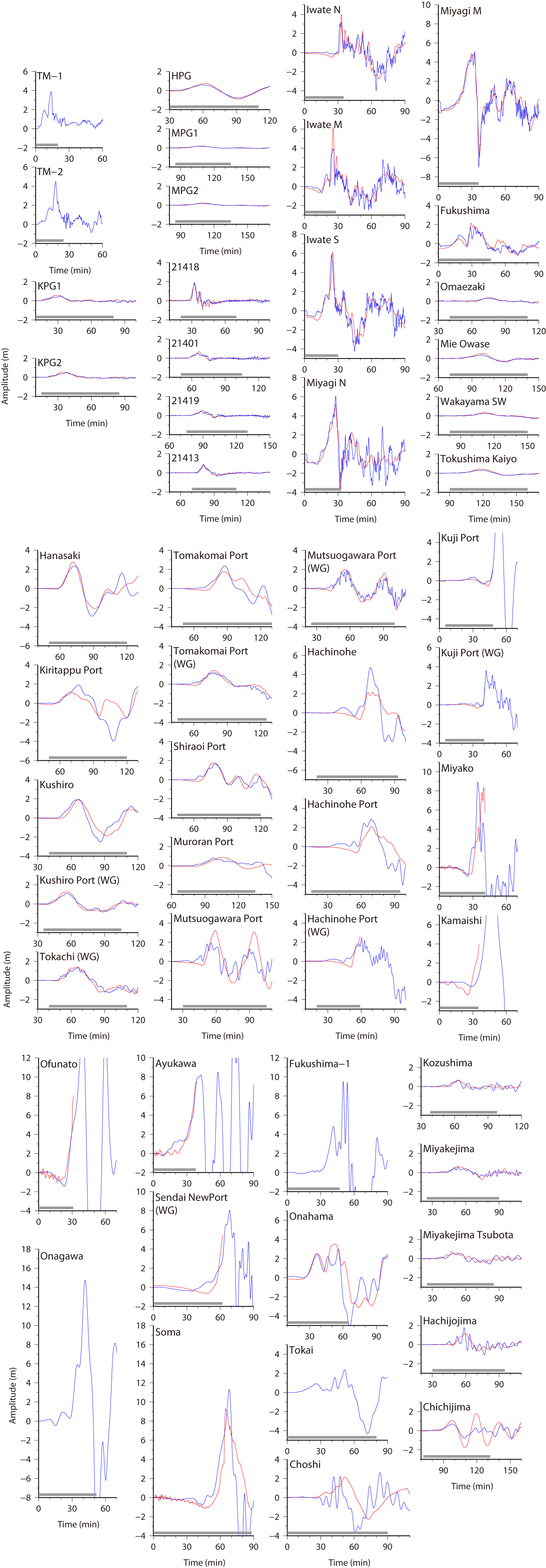
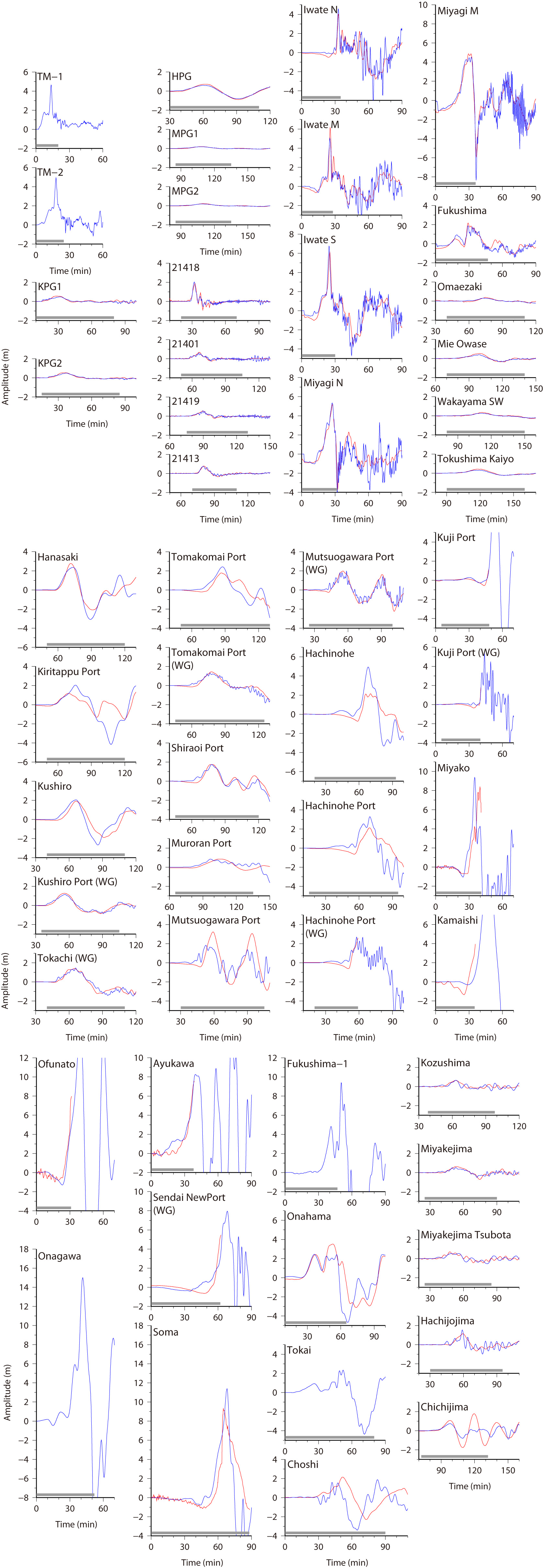
Fig.3 Tsunami Waveforms Fig.3 Tsunami Waveforms Fig.3 Tsunami Waveforms

Fig.3 Simulated Tsunami around Japanese coasts, Left: Ver. 6.2, Middle: Ver. 7.0, Right: Ver. 8.0
 Red and blue lines indicate the observed tsunami waveforms and synthetic ones, respectively. Gray bars show the time windows used for inversion.


 

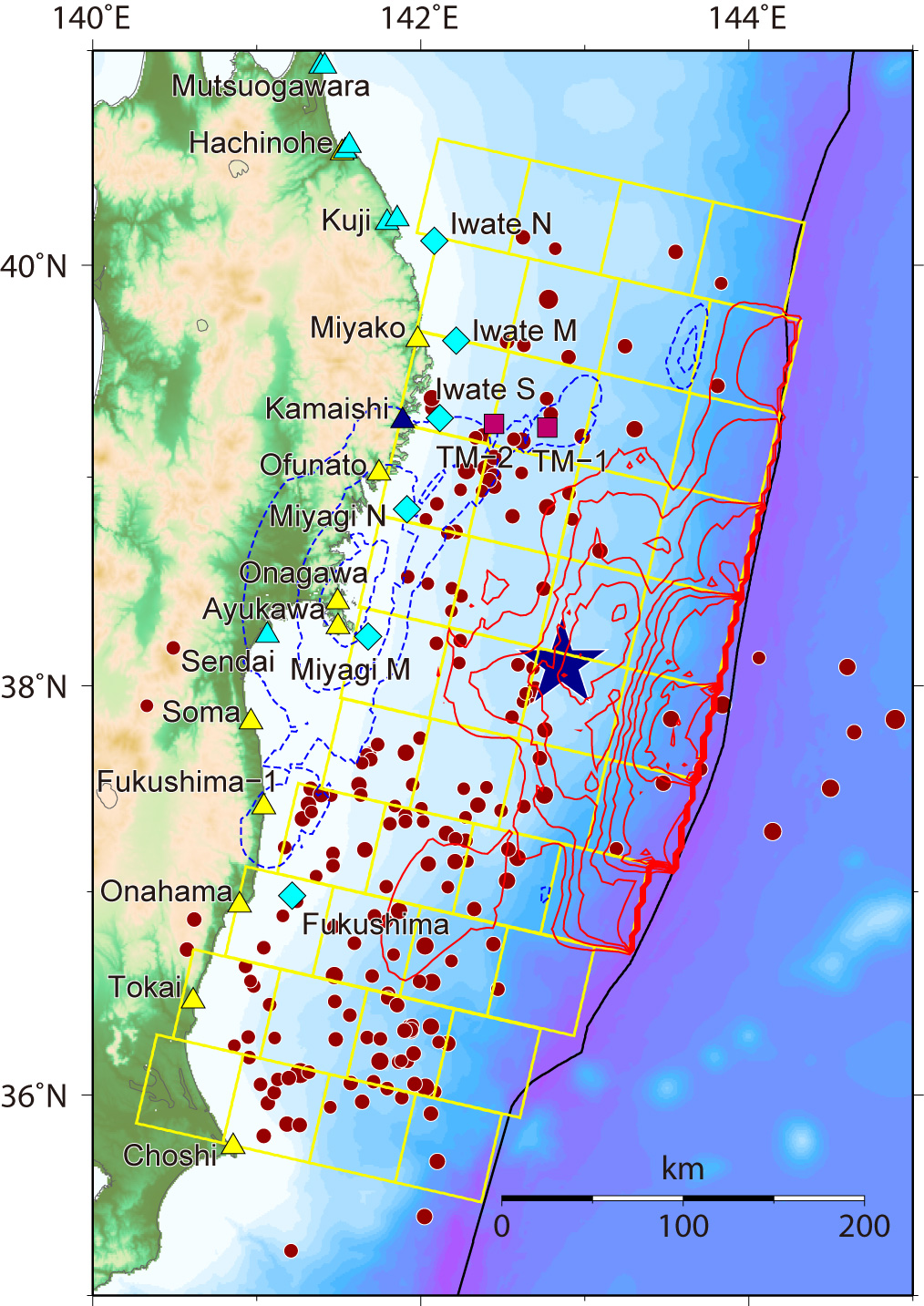
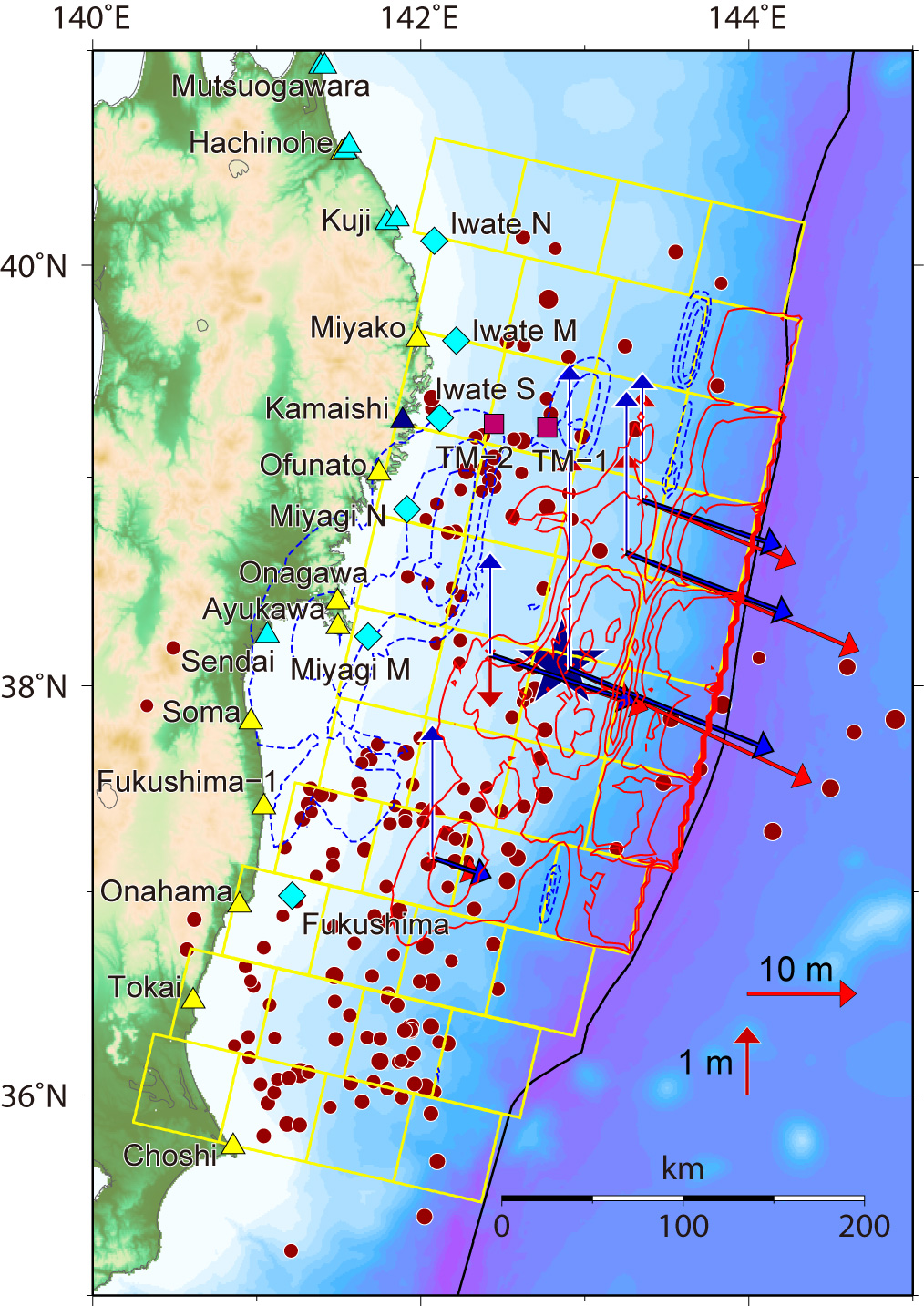
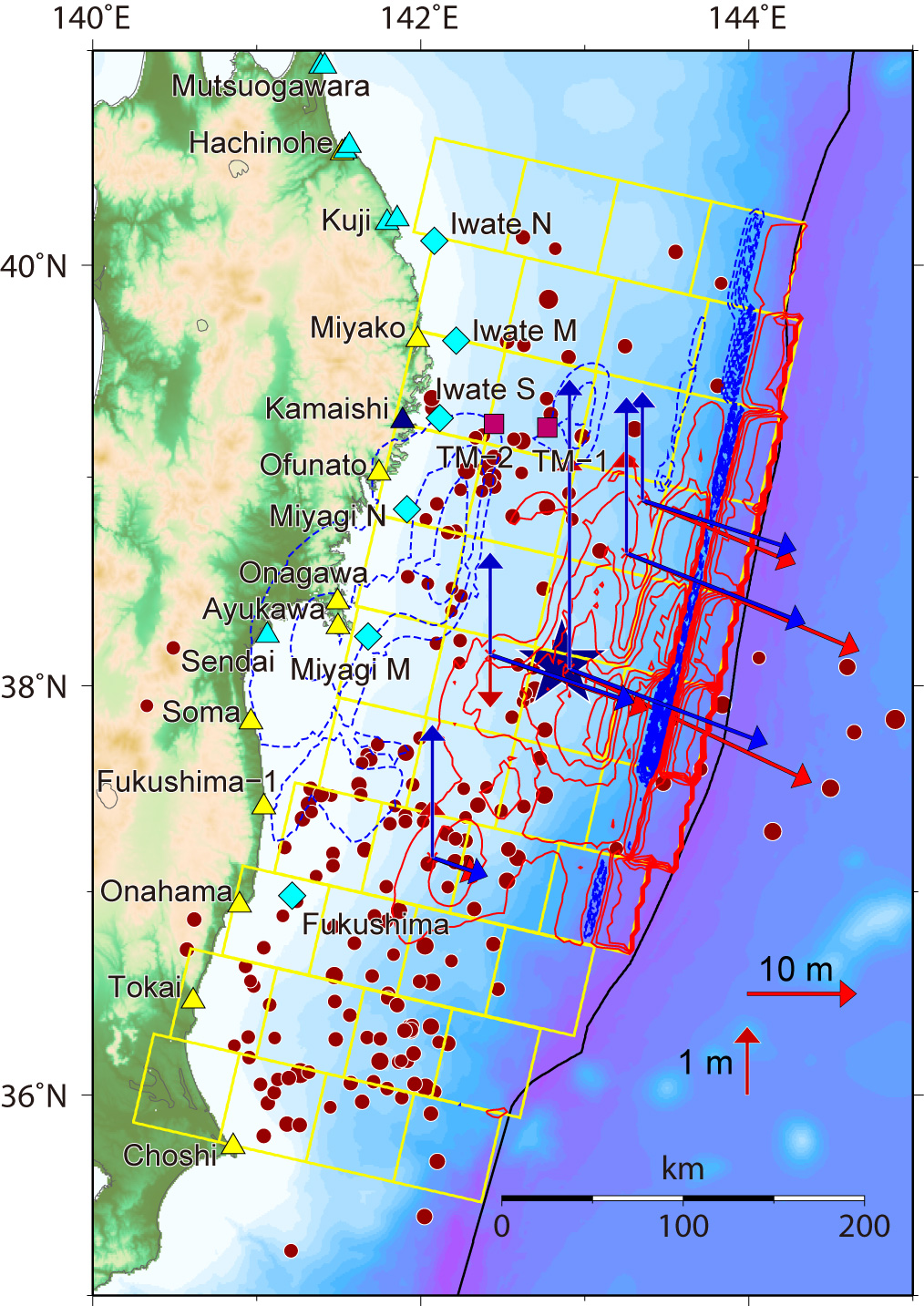
Fig.4 Seafloor Deformation Fig.4 Seafloor Deformation Fig.4 Seafloor Deformation

Fig.4 Seafloor Deformation, Left: Ver. 6.2, Middle: Ver. 7.0, Right: Ver. 8.0
 Calculated seafloor deformation due to the fault model. The red contours indicate uplift with the contour interval of 1.0 m, while the blue contours indicate subsidence with the contour interval of 0.5 m.
Observed displacements by the GPS/A measurements [Sato et al., 2011] are compared with the predicted displacements by the inversion models.


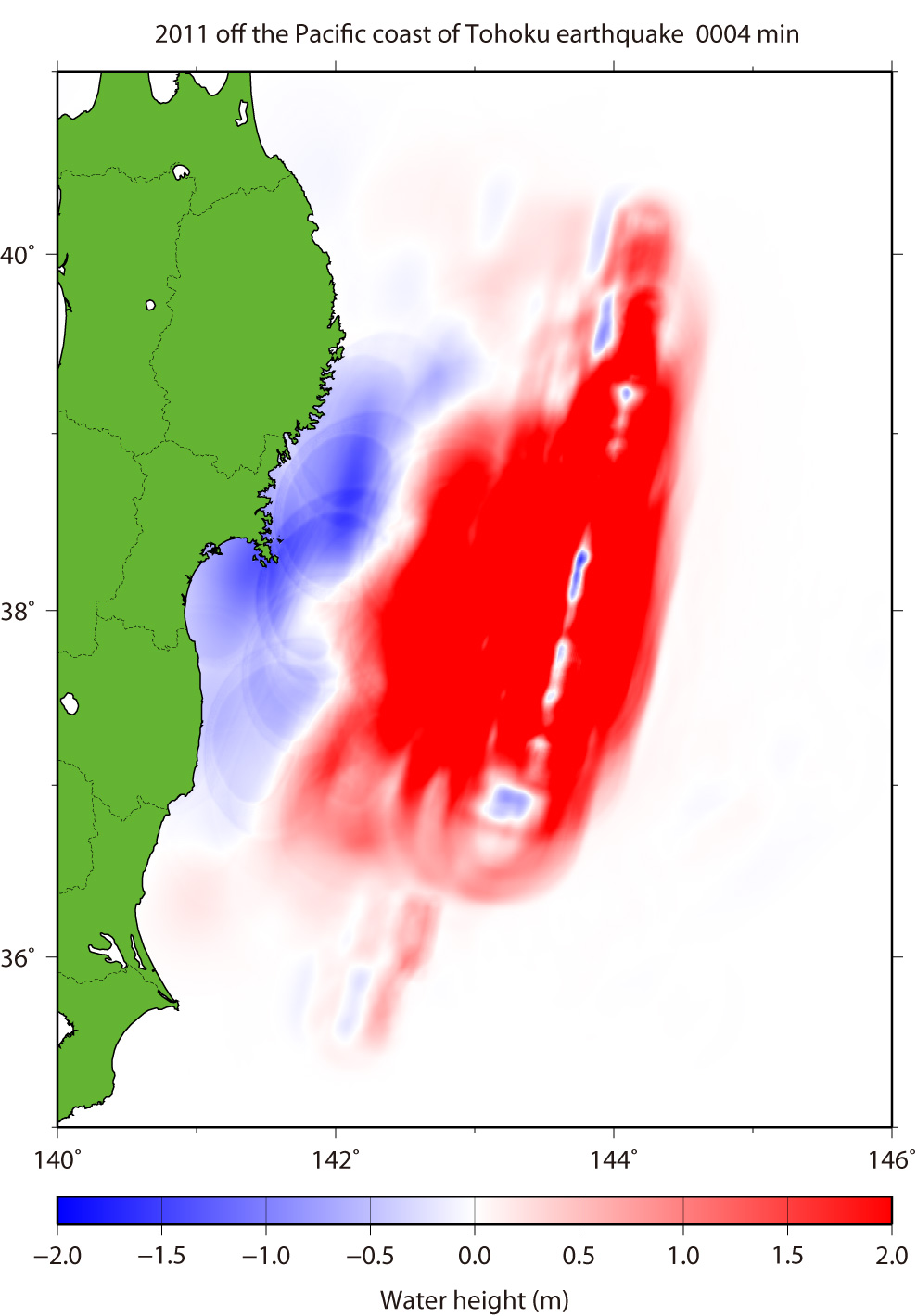
Fig.5 Tsunami propagation

Fig.5 Tsunami Propagation (Click to start animation) for Ver. 8.0
 The red color means that the water surface is higher than normal sea level, while the blue means lower.


 

by Yushiro Fujii (IISEE, BRI) and Kenji Satake (ERI, Univ. of Tokyo)
 
 
References
Nakajima, J. and Hasegawa, A. (2006). Anomalous low-velocity zone and linear alignment of seismicity along it in the subducted Pacific slab beneath Kanto, Japan: Reactivation of subducted fracture zone? Geophys. Res. Lett., 33, L16309, doi:10.1029/2006GL026773
Okada, Y. (1985), Surface Deformation Due to Shear and Tensile Faults in a Half-Space, Bull. Seismol. Soc. Am., 75, 1135-1154.
Satake, K. (1995), Linear and Nonlinear Computations of the 1992 Nicaragua Earthquake Tsunami, Pure and Appl. Geophys., 144, 455-470.
Satake, K., Fujii, Y., Harada, T. and Namegaya Y. (2013),Time and Space Distribution of Coseismic Slip of the 2011 Tohoku Earthquake as Inferred from Tsunami Waveform Data, Bull. Seismol. Soc. Am., accepted.
Sato, M., Ishikawa, T., Ujihara, N., Yoshida, S., Fujita, M., Mochizuki, M. and Asada, A. (2011). Displacement above the hypocenter of the 2011 Tohoku-Oki earthquake. Science, 332(6036), 1395-1395.


Last Updated on 2012/8/17