Formulation for the rupture distance

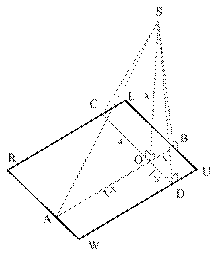R: Reference point

Strike f_s measured from R to L

Dip d measured from R to W

Length: l=AB=RL=UW

Width: w=CD=LU=RW

Distance from the reference point to the observation site: D_rs=RS

Azimuth from the reference point to the observation site: q_s

Coordinate of the vertices:

R: (x_r,y_r,z_r): Reference point of fault

L: (x_r+l sinf_s, y_r+l cosf_s , z_r )

W: (x_r+w cosdcosf_s, y_r-wcosdsinf_s , z_r+wsind)

U: (x_r+w cosdcosf_s+lsinf_s, y_r-wcosdsinf_{s +}lcosf_s, z_r+wsind)

S: (x_r+D_rssinq_s, y_r+D_rs cosq_s , 0.0 ): Observation site

Length of perpendicular SO on the fault plane: SO=x

Parameters (s,t): CO=sCD, BO=tAB

Right triangle DWAS: WS²= WA²+AS²=RW²(1-s)²+AS²

Right triangle DRAS: RS²= RA²+AS²=RW²s²+AS²

WS²- RS²= RW²(1-2s)

Then, s=1/2 – (WS²- RS²)/ 2RW²=1/2 – (WS²- RS²)/ 2w²

Right triangle DRCS: RS²= RC²+CS²=RL²(1-t)²+CS²

Right triangle DLCS: LS²= LC²+CS²=RL²t²+CS²

RS²-LS²= RL²(1-2t)

Then, t=1/2 – (RS²-LS²)/ 2RL²=1/2 – (RS²-LS²)/ 2l²

s<0, t>1 : distance from S to the vertex R

D_rup=RS

s<0, 0<t<1 : distance from S to the side RL

Right triangle DLCS: CS²= LS²-LC²

D_rup=CS=sqrt(LS²-LC²)=sqrt(LS²-LR²t²)= sqrt(LS²-l²t²)

s<0, t<0 : distance from S to the vertex L

D_rup=LS

0<s<1, t>1: distance from S to the side RW

Right triangle DRAS: AS²= RS²-RA²

D_rup= AS=sqrt(RS²-RA²) =sqrt(RS²-RW²s²) =sqrt(RS²-w²s²)

0<s<1, 0<t<1: distance from S to the fault plane

Right triangle DCOS: OS²= CS²-CO²

Right triangle DLCS: CS²= LS²-LC²

D_rup=OS=sqrt(CS²-CO²)=sqrt(CS²-CD²s²)=sqrt(LS²-LC²-CD²s²)
=sqrt(LS²-LR²t²-CD²s²) = sqrt(LS²-l²t²-w²s²)

0<s<1, t<0 : distance from S to the side LU

Right triangle DLBS: BS2= LS²-LB²

D_rup= BS=sqrt(LS²-LB²) =sqrt(LS²-LU²s²) =sqrt(LS²-w²s²)

s>1, t>1: distance from S to the vertex R

D_rup=WS

s>1, 0< t<1: distance from S to the side WU

Right triangle DUDS: DS²= US²-UD²

D_rup= DS=sqrt(US²-UD²) =sqrt(US²-WU²t²) =sqrt(US²-l²t²)

s>1, t<0: distance from S to the vertex U

D_rup=US