Sumatra Tsunami on Oct. 25, 2010  


 

We have simulated the tsunami generated from the the Sumatra earthquake (3.484°S, 100.114°E, Mw = 7.7 at 14:42:22 UTC according to USGS) on Octorbar 25, 2010. The assumed tsunami source is located within the aftershock area during one day after the mainshock (Fig. 1). The fault length and width are 100 km × 50 km. The focal mechanisms are strike:326º, dip:12º, slip:101º from the USGS's Wphase moment tensor solution. The top depth of the fault was assumed to 10 km. The average slip on the fault is 3 m. As the initial condition for tsunami, static deformation of the seafloor is calculated for a rectangular fault model [Okada, 1985] using the source models. The used bathymetry data is basically 2 arc-minute grid and 24 arc-second grids around tide gauges, resampled from GEBCO_08 30 arc-second grid data. To calculate tsunami propagation, the linear shallow-water, or long-wave, equations were numerically solved by using a finite-difference method [Satake, 1995]. The maximum heights of simulated tsunami indicate that the tsunami energy is concentrating to directions perpendicular to the strike of fault (Fig. 2). We have downloaded the DART and tide gauges data from NOAA's and WCATWC's web sites and compared the simulated tsunami waveform and the observed one (Fig. 2). We can see the tsunami propagation in the Indian Ocean (Fig. 3).


 

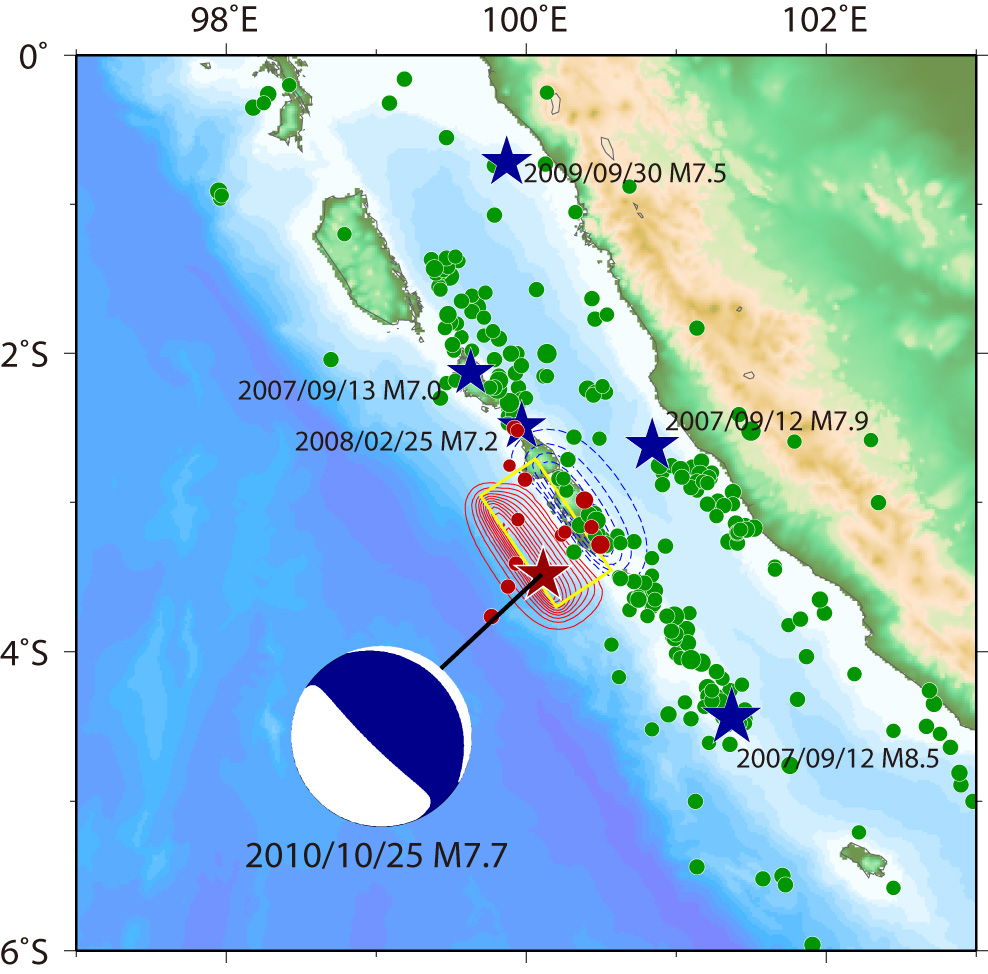
Fig.1 Tsunami Source Model

Fig.1 Tsunami Source Model
 The red contours indicate uplift with the contour interval of 0.1 m, while the blue contours indicate subsidence with the contour interval of 0.1 m. Aftershocks (determined by USGS) during one day after the mainshock are also shown by red circles.


 

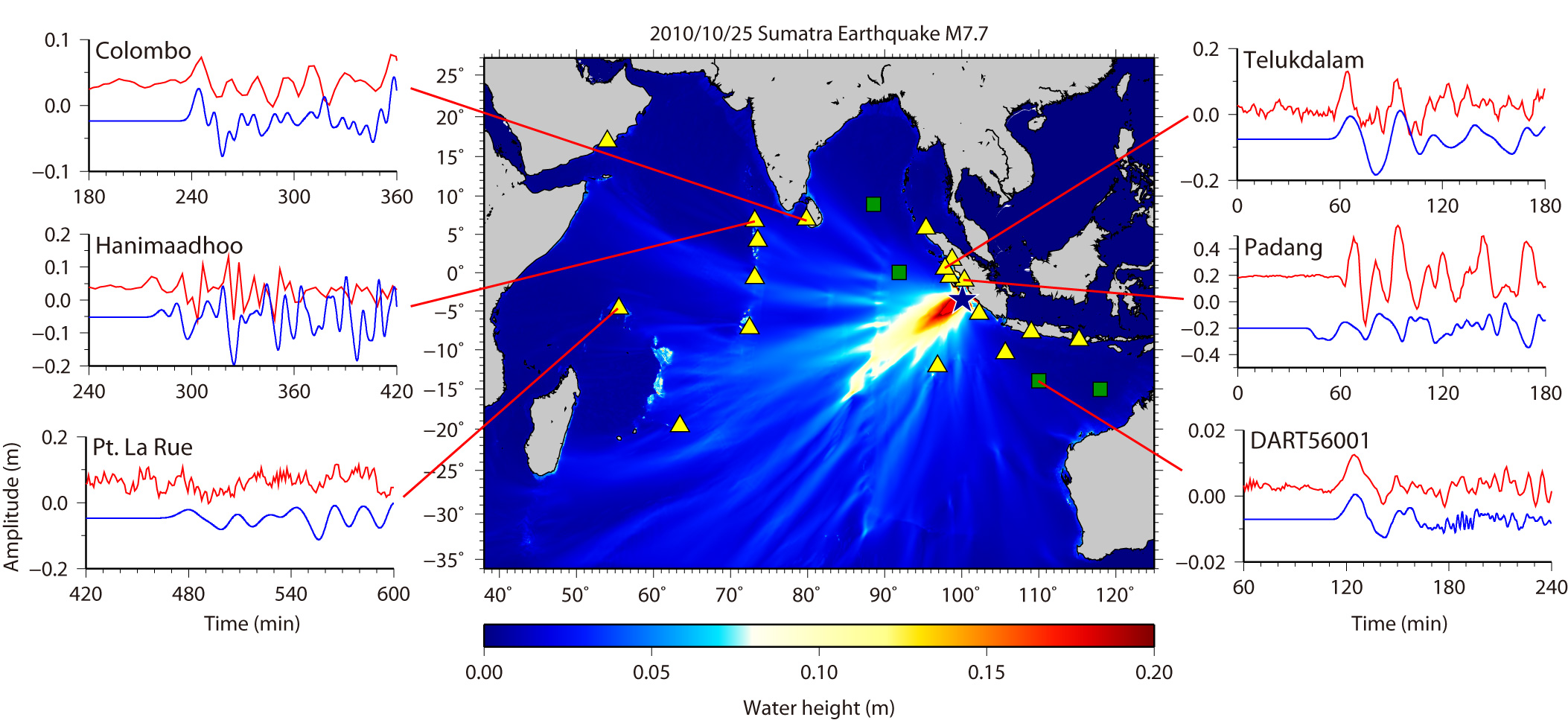
Fig.2 Maximum Height of Tsunami

Fig.2 Maximum Height of Simulated Tsunami
 Solid lines in red and blue indicate the observed tsunami waveform and synthtic ones, respectively.


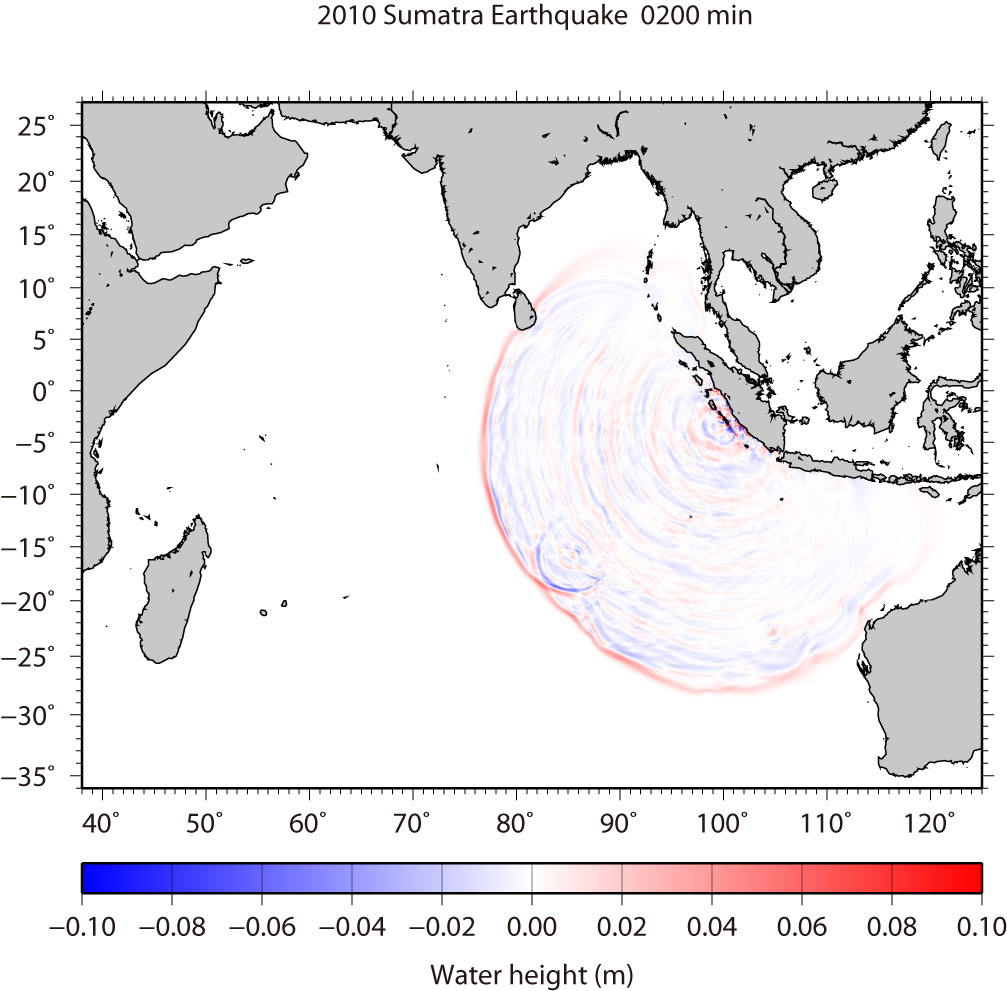
Fig.3 Tsunami propagation

Fig.3 Tsunami Propagation (Click to start animation)
The red color means that the water surface is higher than normal sea level, while the blue means lower.


 

by Yushiro Fujii (IISEE, BRI) and Kenji Satake (ERI, Univ. of Tokyo)
 
 
References
Okada, Y. (1985), Surface Deformation Due to Shear and Tensile Faults in a Half-Space, Bull. Seismol. Soc. Am., 75, 1135-1154.
Satake, K. (1995), Linear and Nonlinear Computations of the 1992 Nicaragua Earthquake Tsunami, Pure and Appl. Geophys., 144, 455-470.


Last Updated on 2010/11/8