We developed a code for dynamic rupture
propagation on arbitrarily shaped faults based on the stress Green’s function
corresponding to a triangular mesh fault element. A boundary integral equation
method is adopted in this study. Starting from representative theorem, after
regularization and descretization of a basic elastodynamic equation relating
stress with slip, a more applicable formulation used in dynamic rupture
simulation is constructed. For a boundary condition, we utilize a simple but
typical slip weakening friction law. In order to avoid numerical oscillation,
according to Courant-Friedrichs-Lewy (CFL) condition, time intervals used in
the simulation is given as Δ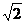t≤
l/6CL (l is the element size, and CL denotes P wave velocity). And then we applied the code to a planar
fault and a curved fault.
For a simple planar fault, spontaneous rupture propagation initiates from a given circular asperity and then propagates symmetrically and bilaterally around the central point. A bump of slip distribution near the center of the fault is the most characteristic feature of the fault that starts from a finite asperity. In addition, we considered a curved fault with different final inclination angles. The curved fault with a small inclination angle does not have significant effects on the rupture propagation. The rupture still can expand symmetrically and bilaterally beyond a bend. However, a large inclination angle may cause the rupture to propagate asymmetrically. Initial conditions determine the rupture propagation behavior. Given the same initial stress on the same fault, the smaller the critical slip weakening displacement is, the faster and longer the rupture propagates. Initial stresses inside and outside of the asperity (Tasp, Te) also have great effects on the rupture propagation. If Te is too small, the rupture will stop soon after initiation. If Te becomes larger, the rupture can propagate longer and faster with subshear velocity.